How Do Row Operations Change The Determinant

Minors and Cofactors: Row Operations (folio 3 of 3)

Find the post-obit determinant by expanding along the row or column of your pick:

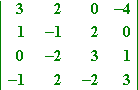
|| 3 2 0 -4 || 1 -1 2 0 || 0 -2 3 1 || -1 2 -2 3 ||

No item row or cavalcade looks any better (easier) to expand along than the others. I think I'll do some row- (and column-) operations first, to get some more than zeroes in the determinant.

row operations

Ah! That'south much nicer. At present I tin can aggrandize along the start row or along the start or 2d column, and my computations will be much easier than if I'd stuck with the original determinant.

I think I'll go down the first cavalcade. The only cofactor I really demand to compute is A _ii,1 :

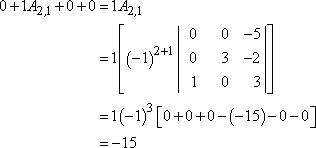
0 + 1(A_2,1) + 0 + 0 = 1(-1)^(2+1)|| 0 0 -5 || 0 3 -2 || 1 0 3 || = 1(-1)(15) = -15

And then the value of the determinant is �xv .

I mentioned that at that place are other ways to manipulate determinants. You can do the other row operations that you're used to, but they change the value of the determinant. The rules are:

If you interchange (switch) two rows (or columns) of a matrix A to get B ,
then det( A ) = �det( B ) .

If y'all multiply a row (or column) of A by some value " chiliad " to get B ,
then det( A ) = (ane/ 1000 )det( B ) .

In other words, if you lot multiply a row (or cavalcade) without calculation it to another row (or column), and then you have to keep track of that multiplier, and split up it off in the terminate. And if you switch two rows (or columns), yous accept to change the sign on the answer in the finish.

The trouble with these rules is that it'south piece of cake to lose rail of whatsoever you multiplied by and how many times you've switched rows, which is why I endeavour to stay away from those operations. But if you're conscientious, these other operations tin can be handy. Returning to that concluding determinant (above), look at these row switches: Copyright � Elizabeth Stapel 2006-2011 All Rights Reserved

switching rows 1 and 2, and then switching rows 2 and 4

I did ii row switches, so I've got two sign changes, which takes me right back to the original sign. And now, expanding down the first column, I get:

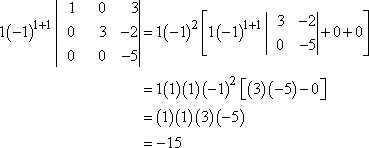
1(-1)^(2+1) || 1 0 3 || 0 3 -2 || 0 0 -5 || = ... = (1)(1)(3)(-5) = -15

Did you see that? Past manipulating the determinant into triangular form, the value of the determinant turned out to be the product of the values on the diagonal (times the two sign changes, which didn't actually change annihilation).

Multiplying along the diagonal is much simpler than doing all the minors and cofactors. Given the opportunity, it is nigh always better to do row operations and only then do the "expansion". Unless you have an instructor who admittedly insists that you aggrandize determinants in their original course, effort to do some row (and column) operations kickoff. If yous're having to practice determinants past hand, doing operations start volition make your life a little less messy.

We've already seen some determinant rules. Two more are as follows:

For matrices A and B , det( AB ) = det( A )det( B ) .

If A is n -by- north , then det( kA ) = k ⁿ det( A ) .

We have also seen that the determinant of a triangular matrix C is just the production of the elements on the diagonal. This tells us that the determinant of the identity matrix I is det(I) = ane . And this leads to a sometimes-useful result:

Any invertible matrix A has an inverse matrix A ^�ane such that (A)(A ^�1) = (A ^�1)(A) = I . Since det(AA ^�one) = det(I) = 1 , and then, whatever the value of det(A) is, the value of det(A ^�1) must exist the reciprocal of det(A) . For case, if det(A) = ii/iii , and so det(A ^�ane) = iii/2 , so det(AA ^�i) = det(A)det(A ^�1) = (2/three)(3/2) = 1 = det(I) .

Merely what if A isn't invertible? Think about it: What number has no reciprocal? The number zero. The only value for det(A) which won't let for A to be invertible is zero. From this we get the following rule:

If a matrix A has no inverse, and so det( A ) = 0 , and vice versa.

You may be asked at some betoken to "determine if the following matrix is invertible past using determinants". The question will be request you to think the above rule, and to see if the determinant is zero or not. Yous will not be expected really to find the inverse.

If you're non going much further in mathematics, yous may be able to get away with having your calculator do about or all of your determinant computations for you. But if you're planning on going on (for instance, to differential equations or linear algebra), and then make sure you lot learn how to do determinants by hand. Yous volition almost certainly need the skill.

<< Previous Top | 1 | 2 | 3| Render to Alphabetize

Cite this commodity as:

Stapel, Elizabeth. "Minors and Cofactors: Row Operations." Purplemath. Available from
https://world wide web.purplemath.com/modules/minors3.htm. Accessed